Backprop Implementation

Backprop is a dynamic programming hack to store the local derivatives for each neuron in the forward pass, and use them during the backward prop. This way we only calculate the local gradients only once as compared to calculating the same gradients for all different combinations of weights. We also express the gradient of weights of a particular layer in terms of gradients of previous layers(moving backwards). This helps us to reuse the pre-computed local gradients.

Local gradients for a neuron is the derivative of it’s output wrt each of it’s input(weights, biases, previous layer ouput).

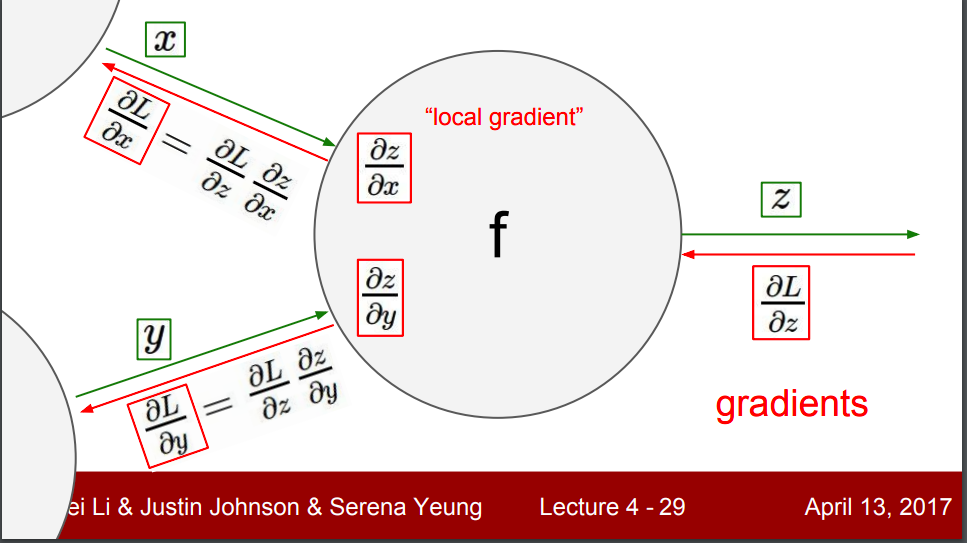
Note: for a neuron, it involoves 2 steps - calculatuing the matmul, and passing the matmul through an activation function. For a neuron with activation function f,

$\frac{\partial z}{\partial w} = X\nabla f$

$\frac{\partial z}{\partial x} = W\nabla f$

For our particular case,

We have one hidden layer with output z1, weight w1, with relu activation(f1). And output layer with output z2, weight w2, and softmax activation(f2).

We use cross entropy loss(J) =

$J = \sum ylog(p)$

Now, to minimize the loss, we have to calculate the gradient of loss function wrt weights of the network, and update the weights accordingly(gradient descent). So we need to calculate -

$\frac{\partial J}{\partial W_1} , \frac{\partial J}{\partial W_2}$

First look at the case for gradient wrt W2. Here, by chain rule, we first calculate the gradient wrt to the output of layer 2, and then gradient of output wrt W2 (local gradient)

$\frac{\partial J}{\partial W_2}= \frac{\partial J}{\partial Z_2}.\frac{\partial Z_2}{\partial W_2}$

So the above equation can be written as -

$\frac{\partial J}{\partial W_2} = \frac{\partial J}{\partial Z_2}. \nabla f_2. Z_1$

Now, when the loss function is cross entropy and the activation function is softmax, the above equation becomes -

$\frac{\partial J}{\partial W_2} = 1/m*(Z_2-y).Z_1$

For calculating the gradient of loss wrt W1:

$\frac{\partial J}{\partial W_1} = \frac{\partial J}{\partial Z_2}.\frac{\partial Z_2}{\partial Z_1}.\frac{\partial Z_1}{\partial W_1}$

We want to see how a change in W1 affects the loss. W1 affects Z1 which affects Z2 which affects the loss. Or we can backtrack the path from loss to W1.

Substituting the local gradient for layer 1 -

$\frac{\partial J}{\partial W_1} = \frac{\partial J}{\partial Z_2}.\frac{\partial Z_2}{\partial Z_1}.\nabla f_1.X$

Substituting the local gradient for layer 2 -

$\frac{\partial Z_2}{\partial Z_1} = W_2\nabla f_2$

So the derivative equation becomes -

$\frac{\partial J}{\partial W_1} = \frac{\partial J}{\partial Z_2}.\nabla f_2.W_2.\nabla f_1.X$

As computed for first gradient, this equation finally becomes -

$\frac{\partial J}{\partial W_1} = 1/m*(Z_2-y).W_2.\nabla f_1.X$

Additional Note:

Derivative of softmax -

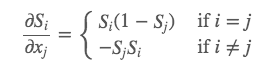
Derivative of sigmoid -

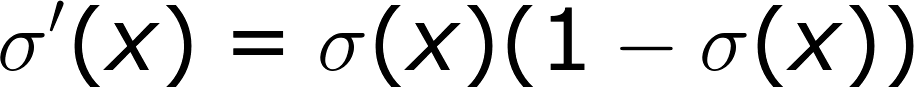
For binary cross entropy with sigmoid activation, the derivative is -

$\frac{\partial J}{\partial W} = 1/m*(y_p-y).X$